GEOMETRICAL CONSTRUCTIONS

Many of the designs on this site contain spirals and self-similar shapes derived from the golden ratio and other geometrical constructions.

Golden Rectangle

Golden Rectangle construction showing self-similar subdivision pattern

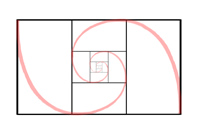
The golden ratio has a natural self-similarity. It is defined by that rectangle which can be partitioned into a square plus a remaining area having the same proportions as the original rectangle. There is only one rectangle that satisfies this requirement and the proportions of the rectangle are the golden ratio φ = 1.618... The smaller rectangle can be further subdivided in the same way, over and over again, to create a self-similar object. The inscribed curve (which passes through the intersection of the straight lines), is called the "golden spiral". This is a logarithmic spiral defined by r ∝ exp(bθ) where b = (2/π)ln(φ). This construction is also related to the Fibonacci numbers.

√2 Rectangle

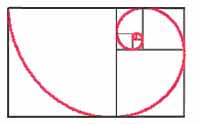
√2 Rectangle construction showing subdivision into two equal copies

A similar construction can be made by defining the rectangle that can be partitioned into exactly two smaller copies of itself. The proportions of this rectangle are √2. Again, this subdivision can be repeated indefinitely. The corresponding logarithmic spiral is specified by r ∝ exp(bθ) with b = (2/π)ln(√2).

Silver Rectangle

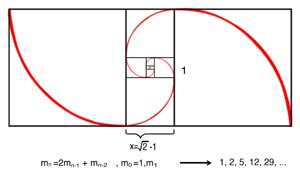
Silver Rectangle construction showing Pell number relationships

Yet another construction can be made by considering a rectangle which is replicated when a square on each end leaves a remaining area that has the same proportions as the original shape. This proportion is known as the silver ratio, δ = (1+√2). As suggested in the figure, the ratios of the sides of the squares leads to the Pell numbers. The inscribed spiral is another logarithmic spiral with b = (2/π)ln(δ).

√3 Rectangle

√3 Rectangle construction showing division into three equal areas

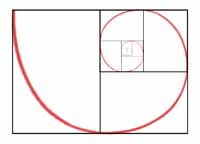
Here is a construction that divides the rectangle into three equal areas all the same shape as the original. The ratio of the sides of this rectangle is √3, and the logarithmic spiral is specified by b = (2/π)ln(√3).

Golden Triangles

Golden Triangles construction based on equilateral triangles

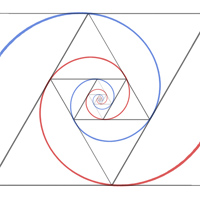
Finally, an analogous construction based on equilateral triangles instead of rectangles. The ratio of one triangle to the next is the golden ratio, φ. But, the inscribed spiral is different from the golden spiral. Here, r ∝ exp(bθ) with b = 3/(2π)ln(φ).